こちらのページは日本語に自動翻訳したものです。 元の英語を表示しますか？
この翻訳は役に立ちましたか？
  1. Home
  2. Technology
  3. 有限要素解析

有限要素解析

有限要素解析(FEA)は、構造、音響、電磁、または熱性能に関する製品とアセンブリの仮想モデリングとシミュレーションです。FEAは、有限要素法(FEM)の実用的なアプリケーションです。

有限要素解析とは

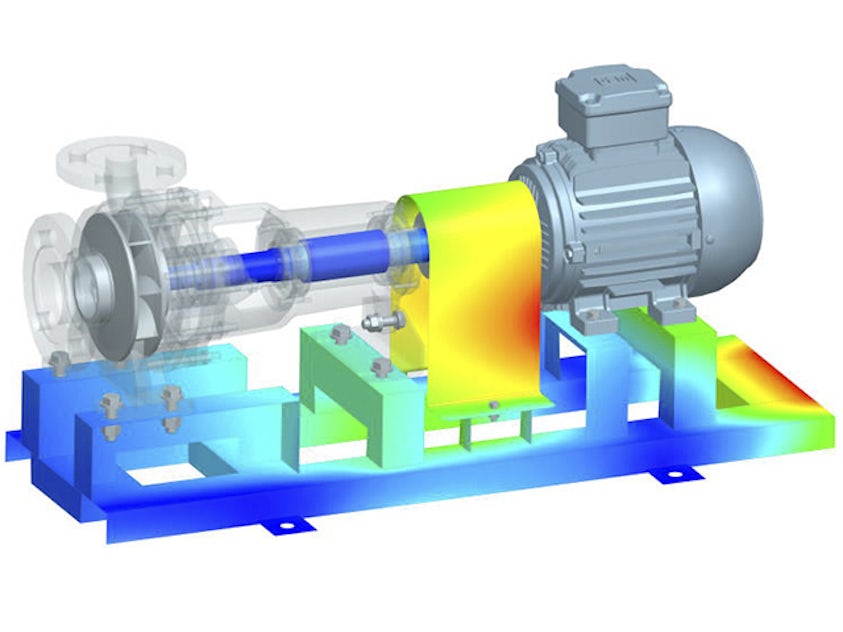
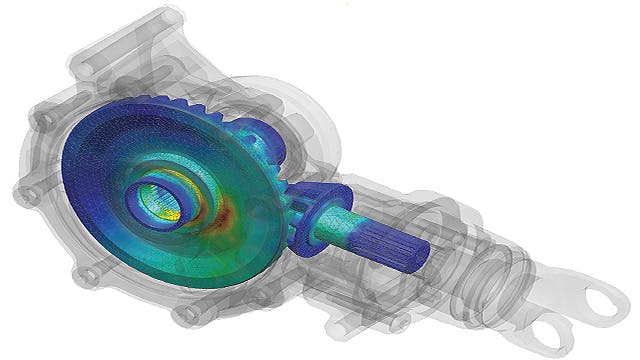
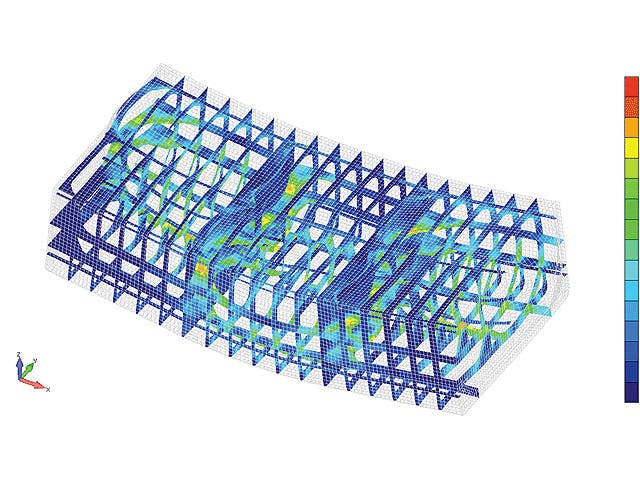
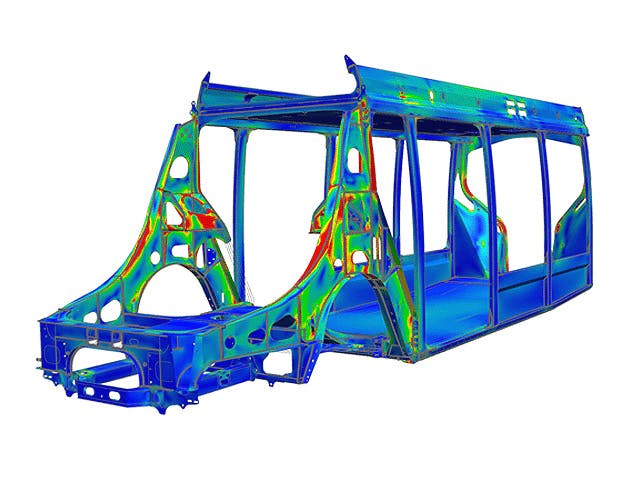
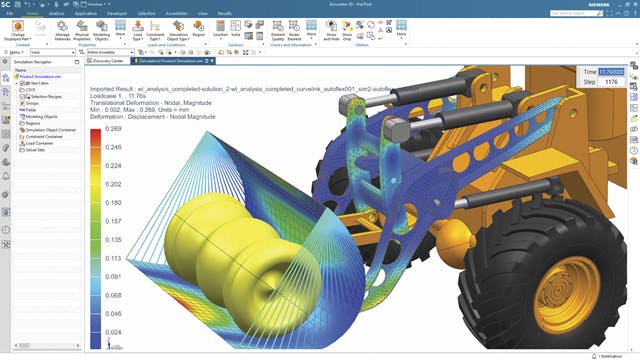
有限要素解析は、仮想環境で製品とシステムをモデル化し、潜在的な(または既存の)製品性能の問題を見つけて解決することです。 FEAはFEMを実用化したものであり、エンジニアや科学者が複雑な構造、音響、電磁気、熱、流体、マルチフィジックスの問題を数学的にモデル化し、数値的に解決するために使用します。FEAソフトウェアは幅広い業界で利用できますが、航空、自動車、電子機器、産業機械、船舶、消費者製品業界で最も一般的に使用されています。

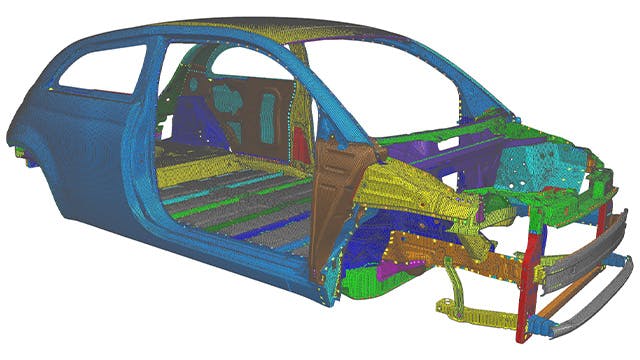
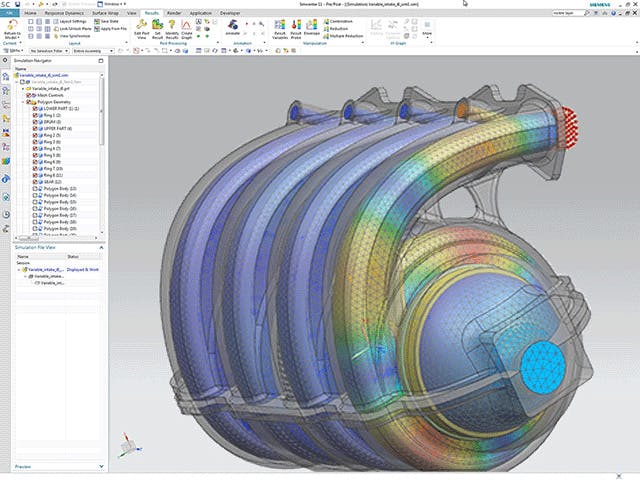
有限要素(FE)モデルは、設計の形状を形成する「ノード」と呼ばれる点のシステムで構成されています。これらのノードに接続されているのは、有限要素メッシュを形成し、モデルの材料特性と構造特性を含み、特定の条件に対するモデルの反応を定義する有限要素です。有限要素メッシュの密度は、特定の領域の応力レベルの予想される変化に応じて、材料全体で変化する可能性があります。 応力の変化が大きい領域は、通常、応力の変化がほとんどまたはまったくない領域よりも高いメッシュ密度を必要とします。 関心のあるポイントとしては、以前にテストされた材料の破壊点、フィレット、コーナー、複雑な詳細、および高応力領域などがあります。

関連製品: Simcenter 3D |Simcenter Nastran |Simcenter Femap |SSimcenter MAGNET |Simcenter E-machineの設計 |NX用Simcenter FLOEFD

Rotating machine structural simulation visual from the Simcenter 3D software.
Engineer Innovation 誌を読む

利点を明らかにする

FEAは、日常製品のエンジニアリング設計と解析析を支援するために、実験的および解析的手法に取って代わったり補完したりするためによく使用される、確立された手法です。プロトタイピングや実験と比較して、FEAベースのシミュレーションには次の利点があります。

パフォーマンスの向上

有限要素解析により、製品性能を向上させるためのエンジニアリングの可能性を迅速に解析し、調査することができます。

作業時間の短縮

有限要素解析は、ビルド&テスト方式よりも迅速に、最適化された製品設計を市場に投入するのに役立ちます。

コスト削減

有限要素解析を活用することで、従来の物理プロトタイプベースのテストプロセスと比較して、製品開発コストを大幅に削減できます。

FEAシミュレーションプロセスのステップ

使用するソフトウェアに関係なく、ほとんどのFEAシミュレーションはこれらの一般的な手順に従います。

Simcenter 3Dソフトウェアのヒートマッピングビジュアルを使用した自動車フレームの3Dモデル。

Pre-processing

前処理段階では、ジオメトリを編集し、シミュレーション用に準備します。メッシングと呼ばれるプロセスでは、前処理ツールが設計ジオメトリを小さな有限要素に変換してから、材料特性、荷重、拘束条件、およびシミュレーションパラメータを適用します。

FEの前処理/後処理

CFDシミュレーションソフトウェアは、CFDソルバーを使用して離散化された方程式の反復的な解法を開始します。

Solving

FEAシミュレーションソフトウェアは、ソルバーを使用して離散化方程式の反復的な解法を開始します。この手順には多くの時間と演算リソースを必要とします。複雑なシミュレーションの場合、コスト効果の高い選択肢としてクラウドコンピューティングを選ぶ企業が増えています。

機械シミュレーション

Simcenter 3Dソフトウェアによる機械構造ビジュアルの線形解析。

Post-processing

ソルバー処理の後、レポート、測定モニター、プロット図、2D/3D画像やアニメーションなどによりシミュレーション結果を視覚化し、定性的および定量的に解析します。結果の検証と妥当性確認もこの段階に含まれます。

FEの前処理/後処理

FEA解析の種類

1D 解析 (ビーム モデル)

1D 解析とは、ビーム要素など、2 つのノードのみで構成される 1 次元要素のみで作成されたモデルを適用することです。1D 解析は、車体や機体など、通常はモデル化が複雑な構造の初期段階の解析に適しています。1Dビームモデルは、エンジニアが完全な形状をより深いレベルで解析する準備が整う前に、ボディダイナミクスを迅速に評価するのに役立ちます。

2D 解析 (シェル モデル)

エンジニアは、板金で作られた部品など、薄肉ボディ用の四角形要素や三角形要素などの2次元要素を使用してジオメトリをメッシュします。要素プロパティは、ソルバーが応力、ひずみ、その他の結果の計算に使用するシェル要素の板厚を定義します。FEAプリプロセッサには、エンジニアがジオメトリ上にシェルメッシュを作成するのに役立つ高速メッシングアルゴリズムがあります。

3D解析(ソリッドモデル)

エンジンブロックのような固体で分厚い形状の場合、エンジニアは固体の3次元要素を使用して形状を表現します。四面体、ピラミッド、六角形要素は、ソリッド ボディ全体に作成されます。FEAプリプロセッサには、エンジニアがソリッドメッシュモデルを作成するために必要なツールがあります。

マルチフィジックスFEA

最新のFEAは、単一の物理領域を個別にシミュレートするだけではありません。今日、FEAは、流体-構造連成(FSI)、熱-機械シミュレーション、構造FEベースの弾性体によるマルチボディダイナミクス、電気機械-熱など、エンジニアがさまざまな物理を結合できるようにすることで、はるかに分野横断的なものとなっています。マルチフィジックスシミュレーション は、最大のパフォーマンスを達成するために、複数分野にまたがるクロスドメインエンジニアリングを必要とする、ますます複雑化する製品において根本的に重要です。

FEA関連製品を探す

Simcenter 3Dソフトウェアで作成した3Dモデルのビジュアル。
Simcenter

Simcenter 3D software

シミュレーションを効率化して複雑なエンジニアリング課題を解決します。Simcenter 3Dは、複数領域にわたる複雑な製品の性能エンジニアリングを目的とした最も包括的で完全統合型のCAEソリューションの1つです。
Simcenter Femapソフトウェアを使用して作成されたシミュレーションの画像。
Simcenter

Simcenter Femap software

複雑な製品やシステムの有限要素モデルを作成、編集、評価します。Simcenter Femapは、コンポーネント、アセンブリ、システムをモデル化するための高度なCAEプリプロセッサーおよびポストプロセッサーです。
Simcenter Nastranソフトウェアによる車両コンポーネントのCFDシミュレーション。
Simcenter

Simcenter Nastran software

製品の構造強度、振動、音響を正確にシミュレーションします。Simcenter Nastranは、計算性能、正確性、信頼性、拡張性に優れた有限要素法 (FEM) ソルバーです。

FEAソフトウェアを無料で試す

トラクター設計のシミュレーションモデルを表すSimcenter 3Dソフトウェアビジュアル。

Simcenter 3D trial

  • CADジオメトリをシミュレーションに使用可能なジオメトリにすばやく変換
  • 構造解析のためにモデルを効率的にメッシュ化して解析し、設計性能に関する洞察を得る
  • Simcenter 3Dソフトウェアでシミュレーションモデルを迅速に更新して設計変更を行うため、数秒でシミュレーションを再開できます。

よくある質問 (FAQ)

有限要素解析は正確ですか?

有限要素解析(FEA)は、何十年にもわたって製品エンジニアリングに使用されてきました。それに伴い、忠実度の高いモデリング手法やより実用的な手法が継続的に開発され、十分に正確な結果をより迅速に得ることができます。

今日、エンジニアは、最小限の計算労力でエンジニアリングの質問に答えるために、ニーズに最も適した精度レベルを選択することができ、また選択する必要があります。精度のレベルは、実際の動作を数パーセントまたはそれ以下の誤差で予測できる忠実度の高いモデリング手法から、迅速な傾向予測を可能にする迅速な方法まで多岐にわたります。

現在、FEAシミュレーションツールの認証および検証プロセスは十分に確立されています。これらは、FEAの進歩、デジタルツインの信頼性と信頼性、および新しい分野での確立にとって重要な要素であり続けるでしょう。予測シミュレーションは、高価な測定やプロトタイピングの必要性を継続的に減らしますが、実験による厳密なFE手法とベストプラクティスの検証が引き続き必要になります。 

FEAを学ぶのは難しいですか?

FEAを学ぶには、時間、献身、徹底的な研究と実践が必要です。ドメインの基礎となる基礎物理学を理解し、数値的手法とその限界を把握し、実際のFEAソフトウェアツールの実践的な使用を練習することが重要です。しかし最新のFEAソフトウェアにおける自動化、計算能力の向上、ユーザーインターフェースの継続的な改善により、すべてのユーザーレベルで忠実度の高いFEAへの障壁がさらに低下しています。結果の探索とシミュレーションベースの意思決定へと範囲がシフトしています。また、FEAの結果に基づいて結果を判断し、有意義なエンジニアリングの決定を下すために、発生している基本的な物理ダイナミクスを理解することも重要です。

FEAの用途は何ですか?

FEAソフトウェアは、機械物理学と、それが製品やシステムの設計に及ぼす影響を理解または予測する必要がある場合に、幅広いエンジニアリングアプリケーションで使用されています。工業製品の設計では、有限要素解析が複雑な形状のマルチフィジックス挙動をシミュレーションするように進歩しており、企業はプロトタイプを構築する前に製品設計を完全に理解し、仮想的に最適化することができます。

有限要素解析が広く使用されている業界には、次のようなものがあります。

  • 航空宇宙
  • 自動車
  • 消費財を扱う企業は、
  • 船舶(船舶設計、推進システム、エンジン設計)
  • エレクトロニクス
  • エネルギー(原子力、石油・ガス、発電)
  • 組み立てサービス
  • ライフサイエンス
  • ターボ機械
  • スポーツ
  • 構造、振動、電磁気学、音、熱、流体の流れを含むその他の一般的な用途

FEM解析とは

有限要素法は、有限要素解析と同じ意味です。主な違いとして、FEMはより具体的には数学的手法を指します。しかし、多くの人はFEMとFEAという用語を同じ意味で使用しています。

FEMは有限要素モデルを指すためにも使用されることがありますが、これは主にメッシュ(1D、2D、または3D)モデルを意味し、荷重や拘束条件も含みます。

詳細はこちら

見る

オンデマンドウェビナー |従来の有限要素データを再利用してシステムレベルのモデルを作成

オンデマンドウェビナー |シミュレーションとデータ管理による船舶設計の合理化

聴く

ポッドキャスト |Adrian Perregauxによる電気モーターの設計とシミュレーションの進歩

ポッドキャスト |実行可能なデジタルツイン: 機械用のスマートウォッチ

読む

ブログ |Simcenter FEAに関するすべてのブログ

機械シミュレーション |CAEを使用して複数の分野にわたる機械的性能を予測